TypeScript 与集合论
TypeScript 与集合论
本文是 TypeScript and Set Theory 的中文翻译,原文链接:https://ivov.dev/notes/typescript-and-set-theory
将类型视作集合
首先我们知道 TypeScript 是具有类型语法的 JavaScript ,我们在学习 TypeScript 的时候,会遇到诸如 extends, &, |, unknown, never 等一些概念。通常我们会孤立的理解他们。
但是,集合论提供了一个心智模型,现在让我们将类型视作为一个可能值的集合,即一个类型的每个值都可以被认为是一个集合中的元素,这使得一个类型可以与一个集合相比较,根据集合的定义,其元素属于这个集合。
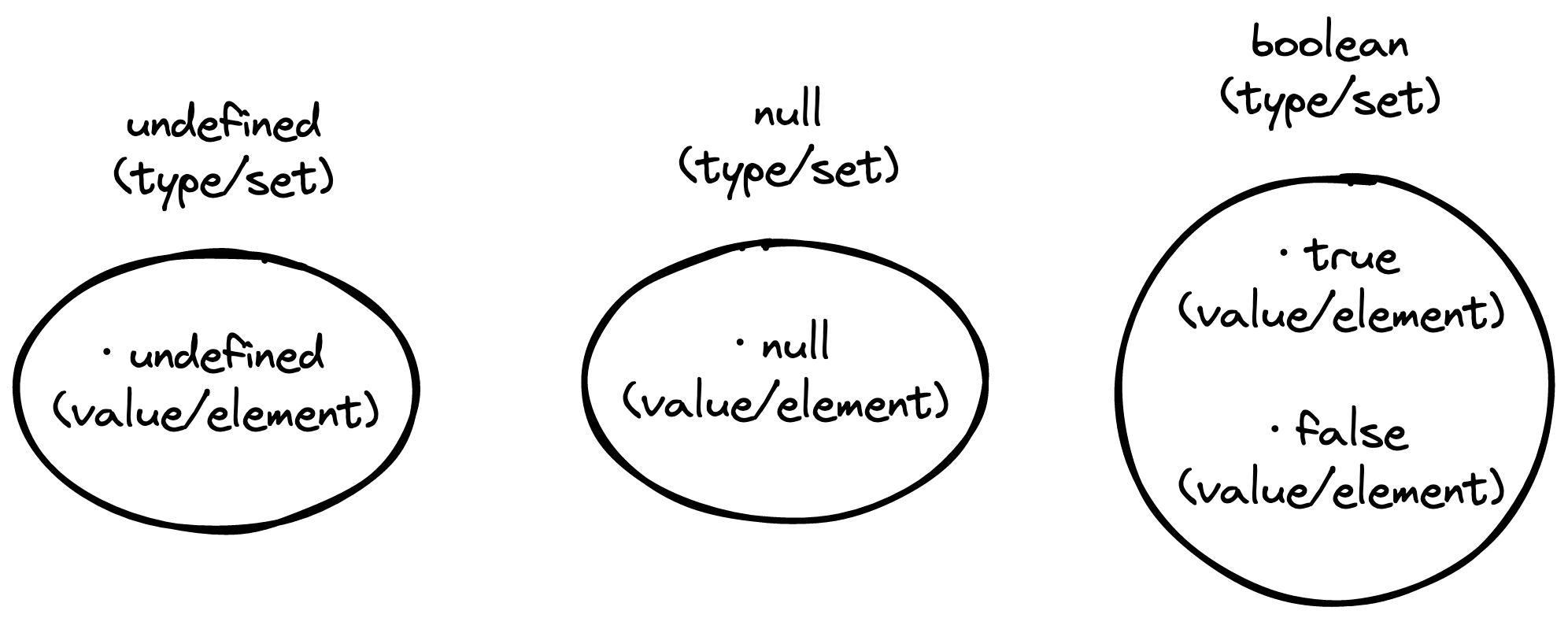
想象一下
number类型是每个可能数字的无限集合string类型是每个可能字符串的无限集合object类型是每个可能对象的无限集合,JavaScript 中,对象包括 function, array, date 等等
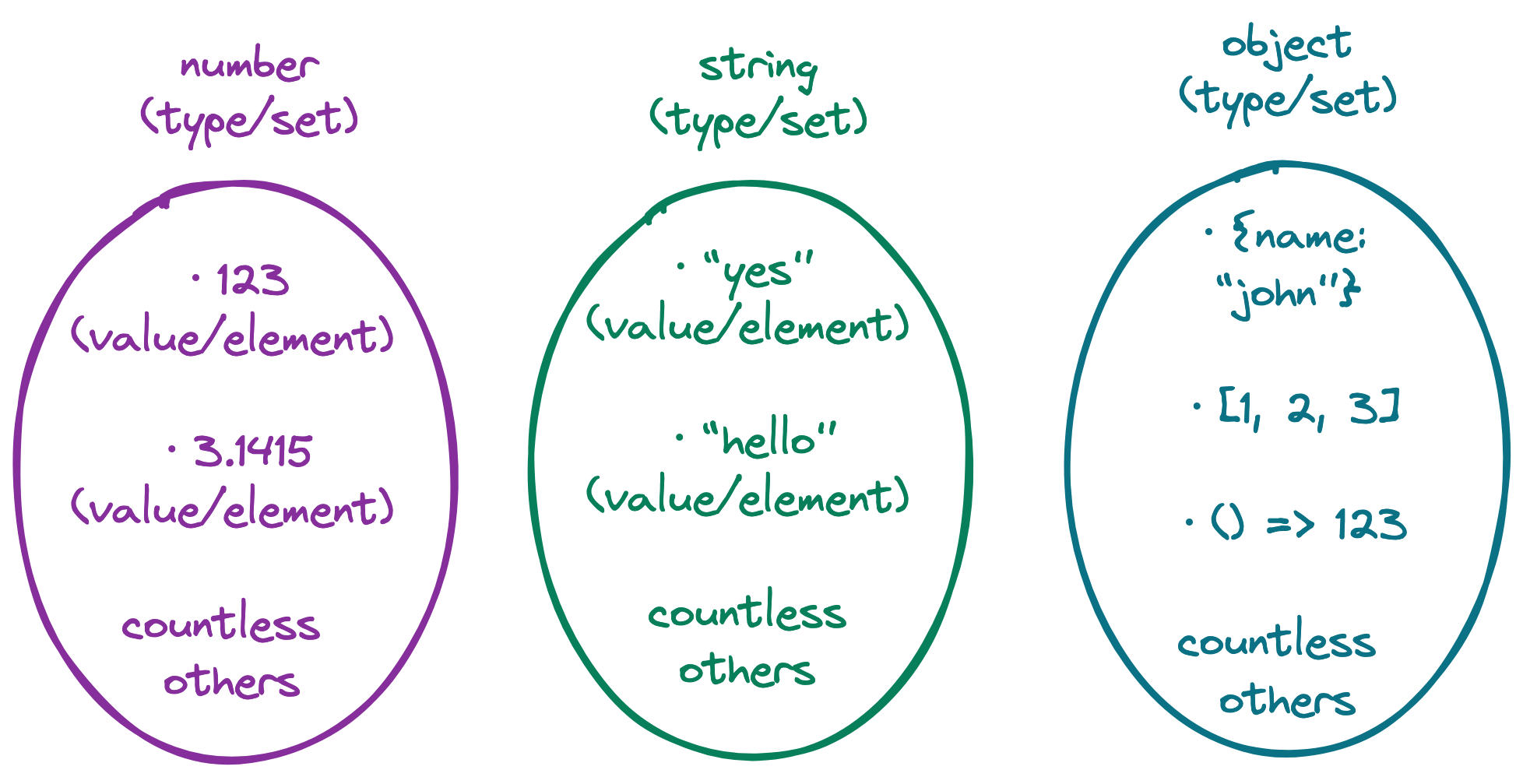
不是所有的被视作集合的类型都是无限的,比如 undefined, null, 和 boolean 类型,它们都是有限元素的集合
想象一下
undefined类型是一个只有undefined元素的集合null类型是一个只有null元素的集合boolean类型是一个只有true和false元素的集合
还有别的有限元素的集合,比如:字面量字符串和字面量字符串的联合类型。下面第一个是包含用户指定的字面量字符串的集合,第二个是包含少量用户指定的字面量字符串的集合。这些都是 string 类型的子集
1 | // both true, string literal ⊂ string |
注意,条件类型中的 extends 相当于
- ⊂:真子集
- ⊆:子集
这在泛型约束中也是如此
1 | // constraint: T ⊂ string or T ⊆ string |
在接口声明中:
1 | interface Person { |
由于 object 类型是任何可能对象的集合,而 interface 是与其属性(properties)匹配的对象的集合,任何给定的 interface 都是 object 的真子集
而反过来,当一个子接口 extends 一个父接口,子接口是与父接口属性匹配的所有可能性的集合。因此,子接口是父接口的真子集,而父接口本身也是 object 类型的真子集
同样注意到,如果一个类型是另一个类型的真子集,那么也暗示了它们在赋值上的兼容性
1 | let myString: string = 'myString'; |
这些和其他编译行为都可以用集合理论来解释
将类型视作集合可以帮助我们进行以下推理:
- 在赋值时的类型兼容性
- 通过类型操作符创建类型
- 解析条件类型
Part1: 赋值兼容性
赋值将一个值存储在标有变量的特定内存位置,值和变量都是类型化的,因为赋值兼容性取决于两个因素:值的类型和变量的类型
当两种类型是相同的时候,就可以进行赋值了
1 | let a: number; |
但是当两个类型不完全相同的时候,为了使赋值成功,必须发生类型转换。当我们把一个类型的值赋值给一个不同类型的变量时,会发生类型转换,也就是说,我们令值的类型成为变量的类型
类型转换通常采取向下兼容的形式:我们将一个类型的子集赋值给匹配这个类型的变量,比如:我们将字面量字符串赋值给 string
1 | let myString: string = 'myString'; |
将一个子类型向上转化为一个父类型,也就是说,一个子集赋值给一个父集。TypeScript允许这种转换,因为它是类型安全的:如果一个集合是另一个集合的子集,那么小集合中的任何元素也是大集合中的成员。
另一方面,降级通常是不允许的。为了确保类型安全,我们不能声明一个大集合的成员也是一个小集合的成员–我们无法确定这一点。而如果两个集合都是相等的,那么这两个类型是相同的,所以不需要进行类型转换。
把上面的赋值反过来,就可以看出,把 string 类型赋值给字面量字符串是不允许的。
1 | let myString: string = 'myString'; |
按照这个逻辑,我们知道在赋值过程中哪些类型转换是被允许的,但是有两种情况除外
从赋值兼容性来讲,never 是特殊的情况:
never可以被赋值到任何类型- 没有一种类型可以被赋值到
never
这意味着任何类型都可以最终接收 never,但是 never 不能接收任何类型。换句话说,任何类型都可以向下兼容 never,但是 never 不能向下兼容任何一个类型。nerver 因此被称为 bottom type
在集合理论中,never是没有任何元素的集合,也没有任何子集——never 是空集
1 | const a: never = 1; // downcasting fails, not assignable |
使用
never赋值是不合理的尽管
never是所有集合的子集,但是在实践中,没有将never赋值给另一个类型的例子。因为根据定义,never类型的值是不存在的——没有一个真正存在的值,它的类型是never但是,如果实践中
never类型的值是不能赋值的,那么never可以被赋值到另一个类型是什么意思?请参考这个答案
与之相反的是 unknown,多数用于标记一个值,其类型需要在使用前被确认。比如:JSON.parse() 最好应该返回 unknown 。TypeScript 强制 unknows 类型的值需要在使用前确认类型
1 | let a: unknown; |
赋值兼容性方面,unknown 有特殊的一面:
- 任何类型都可以被赋值到
unknown unknown不可以被赋值给任何类型
有趣的是,刚好与前面的 never 相反
unknown 可以接收任何类型,但是没有类型可以接收 unknown。换句话说,unknown 可以向下兼容任何类型,但没有类型可以向下兼容 unknown
由于 unknown 需要在使用前确认类型,unknown 可能是任何类型,每个类型就像在 unknown 的保护伞之下。因此 unknown 被称之为 top-type
any被视作逃逸类型奇怪的是,
any像是unknown和never的结合体。任何类型都可以被赋值给any,同样any也可以被赋值给任何类型。作为两种特殊规则的混合体,any在集合论中没有等价物,所以最好把any视作为逃逸类型(不受 TypeScript 约束)
Part2: 创建类型
我们可以使用集合运算符来将现有的集合组合成一个新的集合
- A、B 的并集表示至少在 A 或 B 中所有元素的集合
- A、B 的交集表示同时在 A 和 B 中所有元素的集合
- A、B 的差集表示所有在 A 中但是不是 B 的元素的集合
- A 的反集表示全集 U 中不在 A 的所有元素的集合
用图像描述
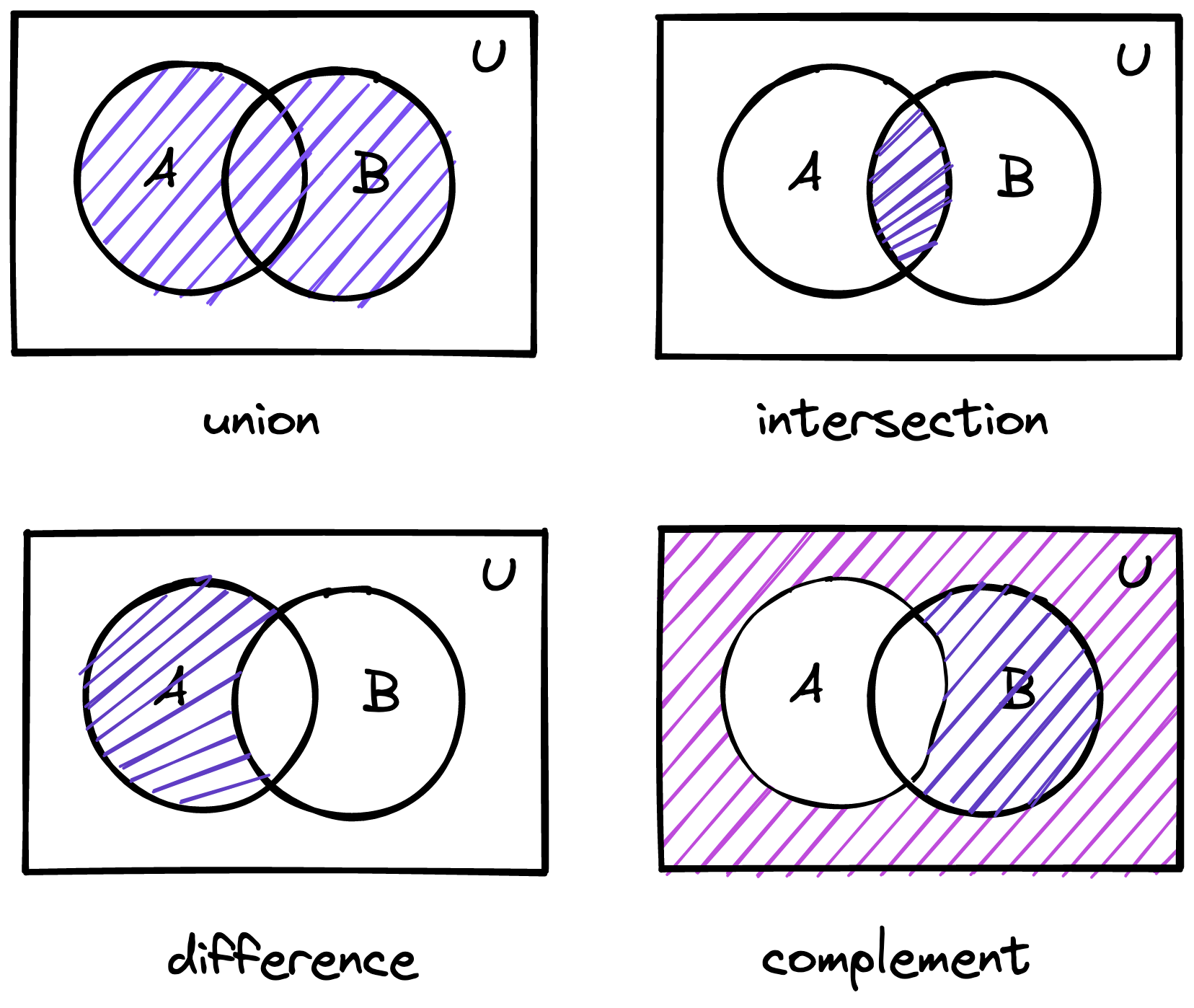
在这四个集合运算符中,TypeScript 实现了两个作为类型运算符
|用于并集&用于交集
与 | 联合意味着创建一个由两种输入类型组成的更广泛、更具包容性的类型
与 & 相交意味着创建一个由两种输入类型共享的元素组成的更小、更具局限性的类型
作为类型操作符,| 和 &操作的是类型(集合) ,而不是属于这些集合的元素(值)。可以将类型操作符看作是接受类型作为参数,并返回另一种类型作为输出的函数
当操作基本类型的时候,|和&的行为是可预测的:
1 | type StringOrNumber = string | number; |
但是操作 interface 的时候,|和&似乎是反直觉的。
思考下面的例子:
1 | type Foo = { |
联合类型 |通常被认为是指“ A 或 B 是可以接受的”,这与布尔运算符 || 在表达式中表示 OR 的事实大致吻合。然而,从 OR 的角度来考虑接口的联合,可能会产生误导
将联合类型 Foo | Bar解析为允许Foo或者Bar的方法是错误的。如上所示,联合类型 Foo | Bar将输出一个 Foo 和 Bar 共同拥有的方法的集合。
反之,对于相交类型也是如此: & 通常被认为“A 和 B”,这与布尔运算符 && 在表达式中表示 AND 的事实大致吻合。然是,从 AND 的角度来考虑接口的联合,可能会产生误导
思考下面的例子:
1 | type Foo = { |
将相交类型 Foo & Bar 解析为允许 Foo 和 Bar 的方法是错误的,如上所示,相交类型Foo & Bar会输出他们的所有元素组成的集合。
总而言之,在联合类型中,用OR的思维方式可能会产生误导,而用更广泛的输出集的方式有助于理解;在相交类型中,用AND的思维方式也会误导,而用较窄的输出集会有助于理解
但是,为什么在联合类型和相交类型中,我们的期望被颠覆了?
对象类型是所有可能性的无限集合;一个接口是具有特定属性的集合。那么,接口就是对象的一个子集,在所有可能性的无限集合中,那些与属性相匹配的对象可以被分配给它
1 | let a: object; |
由于接口描述了一个对象的具体属性,我们给接口添加的属性越多,匹配的对象就越少,所以对应的集合也越小。向接口添加属性会缩小它代表的集合,反之亦然。
1 | interface Person { |
当联合两个接口的时候,我们要创建一个输出类型,接受与之匹配的类型:
- 一个输入类型,或者
- 另一个输入类型,或者
- 它们共同拥有的类型
从所有可能性的集合中,这三种类型被分配到输出类型中,使得输出类型比两个输入类型更广泛,
1 | interface A { |
对于基础类型的联合类型,如 string | number 也会产生重叠,但是没有同时属于两种类型的基础类型,所以没有东西可以被分配给它们重叠的部分。因此我们倾向于忽略这种情况。导致我们默认用布尔操作符 OR 来思考联合类型,但这在对象类型中是错误的!
反过来说,当 interface 相交时,要输出两个 interface 的重叠部分。
1 | interface A { |
对于基础类型的相交类型,如 string | number 永远是空集 never。因为没有基础类型可以与另一个基础类型共享元素。但是接口是对象的子集所以接口的相交类型总是可以产生一个同时满足两个输入的接口。即使相交的接口没有共同属性。
而且,我们将对基础类型的相交的直觉带到了非基础类型上,会导致我们用布尔操作符 AND 来思考。导致我们错误的认为上面 x 和 y 应该成功,而实际上它们不成功
累计效应
当我们联合两个接口,它们重叠部分将会累计属性;
当我们将不同的接口相交时,输出类型会累计属性;
当我们用接口继承另一个接口时,子接口会累计属性。
在所有这三种情况下,这种累积效应类似于接口声明的合并,即同一接口的单独声明创造了一个聚合接口,累积了每个接口中的属性。
Cumulative effect
When we unionize different interfaces, the overlap accumulates properties. When we intersect different interfaces, the output type accumulates properties. When we declare that an interface
extendsanother, the child interface accumulates properties.In all three cases, this cumulative effect resembles that of interface declaration merging, where separate declarations of the same interface create an aggregate interface that accumulates the properties in each.