扁平化数组与树形结构的互相转换
写在前面
今天在做项目的时候,遇到了需要将扁平化数组转换成树形结构的问题。首先第一个想到的是用递归去处理,但是在实际应用的时候,一旦数组长度比较大的时候,性能十分不理想(时间复杂度为0(n^2),能理想就怪了)。后面在查阅资料的时候,发现有更优解,特此记录下来。
先看一下数据:
扁平化数组:
1
2
3
4
5
6
7
| let arr = [
{ id: 5, name: "5", pid: 4 },
{ id: 1, name: "1", pid: 0 },
{ id: 2, name: "2", pid: 1 },
{ id: 3, name: "3", pid: 1 },
{ id: 4, name: "4", pid: 3 },
];
|
树形结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| let tree = [
{
id: 1,
name: 1,
pid: 0,
children: [
{
id: 2,
name: 2,
pid: 1,
children: [],
},
{
id: 3,
name: 3,
pid: 1,
children: [
{
id: 4,
name: 4,
pid: 3,
children: [{ id: 5, name: 5, pid: 4, children: [] }],
},
],
},
],
},
];
|
扁平化数组→树形结构(array to tree)
递归方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
function array2tree(items,rootId) {
let res = []
let getChildren = (res, rootId) => {
for(const i of items) {
if(i.pid === rootId) {
const newItem = {...i, children: []}
res.push(newItem)
getChildren(newItem.children,newItem.id)
}
}
}
getChildren(res, rootId)
return res
}
|
其实思路也很简单,首先传入数组items和根节点ID,然后遍历数组,找到与根节点下的子节点,把子节点push到父节点的children数组里面。然后递归这个过程。。。
显然,这个算法的时间复杂度为O(n^2)
非递归方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
function array2tree(items, rootId) {
const result = [];
const map = {};
for (const item of items) {
map[item.id] = { ...item, children: [] };
}
for (const item of items) {
const id = item.id;
const pid = item.pid;
const treeItem = map[id];
if (pid === rootId) {
result.push(treeItem);
} else {
if (!map[pid]) {
map[pid] = {
children: [],
};
}
map[pid].children.push(treeItem);
}
}
return result;
}
|
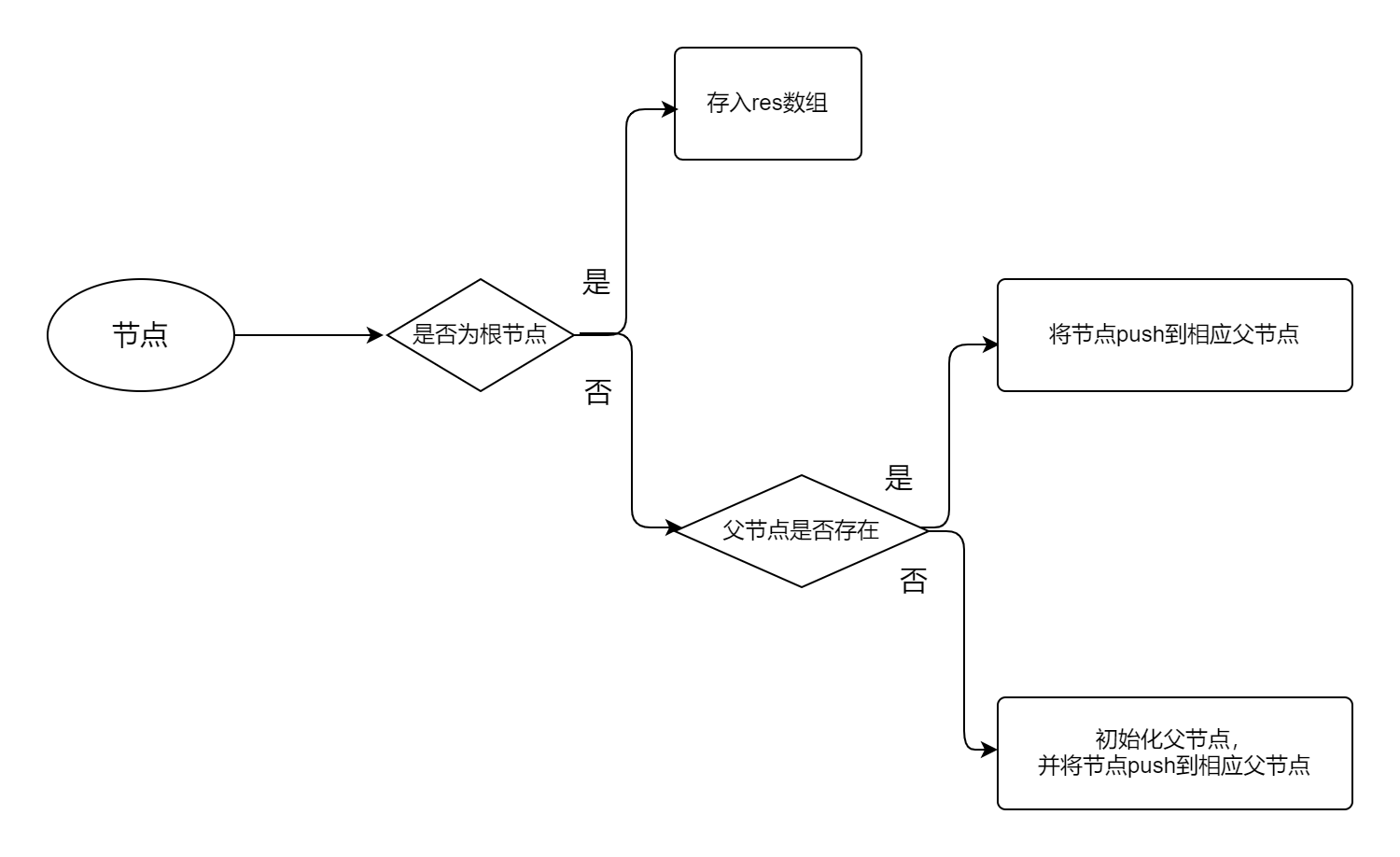
这里说一下思路,先把数组转成以id为key的映射关系。然后再遍历一次数组存入根节点,借助对象的引用,只需要更新map中的children即可。具体可看下面的流程图
显然,时间复杂度为O(n)
最佳性能
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
function array2tree(items, rootId) {
const res = [];
const map = {};
for (const item of items) {
const id = item.id;
const pid = item.pid;
if (!map[id]) {
map[id] = {
children: [],
};
}
map[id] = {
...item,
children: map[id].children,
};
const treeItem = map[id];
if (pid === rootId) {
res.push(treeItem);
} else {
if (!map[pid]) {
map[pid] = {
children: [],
};
}
map[pid].children.push(treeItem);
}
}
return res;
}
|
边做map存储,边找对应关系
显然,时间复杂度为O(n)
树形数据→扁平化数组(tree to array)
递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
function tree2arr(items) {
let res = [];
items.forEach((item) => {
const { children, ...node } = item;
res.push(node);
if (children && children.length) {
res = res.concat(tree2arr(children));
}
});
return res;
}
|
遍历tree,每一项加进结果集,如果有children且长度不为0,则递归遍历
显然时间复杂度为O(n^2)
总结
Array To Tree
递归方式:每次递归寻找当前节点的子节点,并且需要重新遍历数组,时间复杂度为O(n^2)
非递归方式:利用对象的保存是引用这个特点,通过map保存节点及其子节点的信息,只需要将根节点存入数组,即可得到整个树形数据。时间复杂度是O(n)
